```r
#--- loading ---#
library(TENxPBMCData)
all.sce <- list(
pbmc3k=TENxPBMCData('pbmc3k'),
pbmc4k=TENxPBMCData('pbmc4k'),
pbmc8k=TENxPBMCData('pbmc8k')
)
#--- quality-control ---#
library(scater)
stats <- high.mito <- list()
for (n in names(all.sce)) {
current <- all.sce[[n]]
is.mito <- grep("MT", rowData(current)$Symbol_TENx)
stats[[n]] <- perCellQCMetrics(current, subsets=list(Mito=is.mito))
high.mito[[n]] <- isOutlier(stats[[n]]$subsets_Mito_percent, type="higher")
all.sce[[n]] <- current[,!high.mito[[n]]]
}
#--- normalization ---#
all.sce <- lapply(all.sce, logNormCounts)
#--- variance-modelling ---#
library(scran)
all.dec <- lapply(all.sce, modelGeneVar)
all.hvgs <- lapply(all.dec, getTopHVGs, prop=0.1)
#--- dimensionality-reduction ---#
library(BiocSingular)
set.seed(10000)
all.sce <- mapply(FUN=runPCA, x=all.sce, subset_row=all.hvgs,
MoreArgs=list(ncomponents=25, BSPARAM=RandomParam()),
SIMPLIFY=FALSE)
set.seed(100000)
all.sce <- lapply(all.sce, runTSNE, dimred="PCA")
set.seed(1000000)
all.sce <- lapply(all.sce, runUMAP, dimred="PCA")
#--- clustering ---#
for (n in names(all.sce)) {
g <- buildSNNGraph(all.sce[[n]], k=10, use.dimred='PCA')
clust <- igraph::cluster_walktrap(g)$membership
colLabels(all.sce[[n]]) <- factor(clust)
}
```
``` r
pbmc3k <- all.sce$pbmc3k
table(colLabels(pbmc3k))
```
```
##
## 1 2 3 4 5 6 7 8 9 10
## 475 636 153 476 164 31 159 164 340 11
```
``` r
pbmc4k <- all.sce$pbmc4k
table(colLabels(pbmc4k))
```
```
##
## 1 2 3 4 5 6 7 8 9 10 11 12
## 127 594 518 775 211 394 187 993 55 201 91 36
```
Ideally, we should see a many-to-1 mapping where the post-correction clustering is nested inside the pre-correction clustering.
This indicates that any within-batch structure was preserved after correction while acknowledging that greater resolution is possible with more cells.
We quantify this mapping using the `nestedClusters()` function from the *[bluster](https://bioconductor.org/packages/3.21/bluster)* package,
which identifies the nesting of post-correction clusters within the pre-correction clusters.
Well-nested clusters have high `max` values, indicating that most of their cells are derived from a single pre-correction cluster.
``` r
library(bluster)
tab3k <- nestedClusters(ref=paste("before", colLabels(pbmc3k)),
alt=paste("after", clusters.mnn[mnn.out$batch==1]))
tab3k$alt.mapping
```
```
## DataFrame with 16 rows and 2 columns
## max which
## 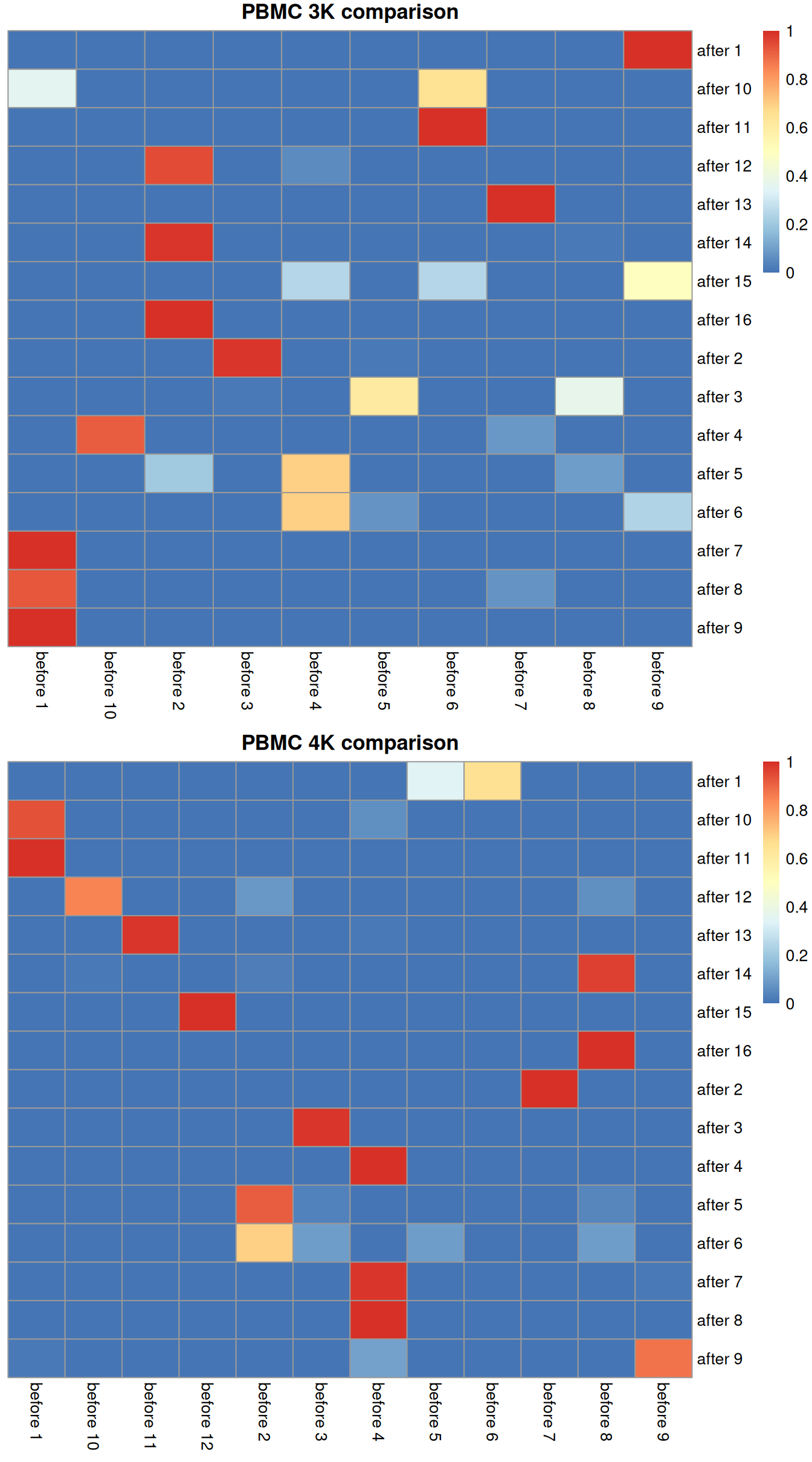
(\#fig:heat-after-mnn)Comparison between the clusterings obtained before (columns) and after MNN correction (rows). One heatmap is generated for each of the PBMC 3K and 4K datasets, where each entry is colored according to the proportion of cells distributed along each row (i.e., the row sums equal unity).
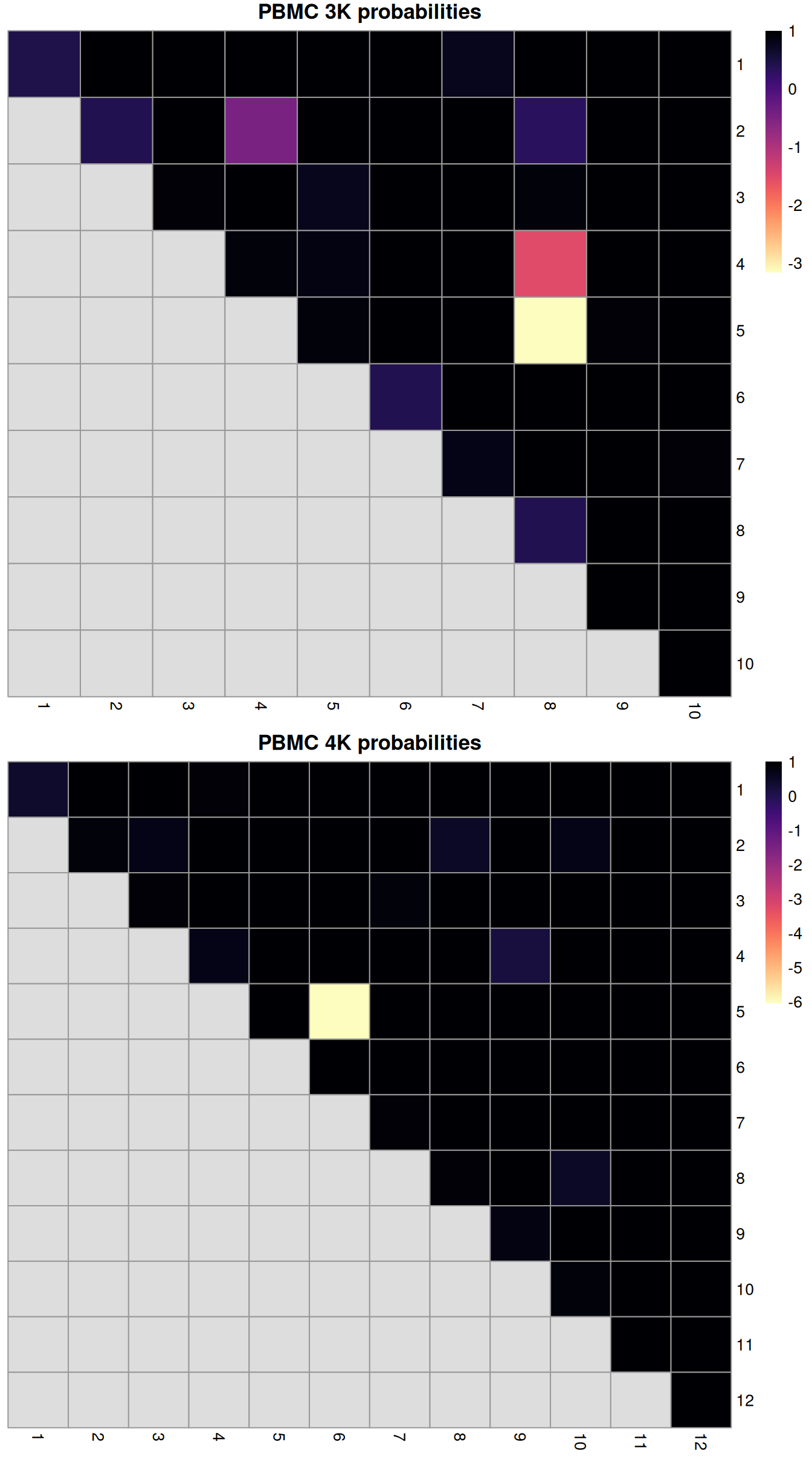
(\#fig:rand-after-mnn)ARI-derived ratios for the within-batch clusters after comparison to the merged clusters obtained after MNN correction. One heatmap is generated for each of the PBMC 3K and 4K datasets.
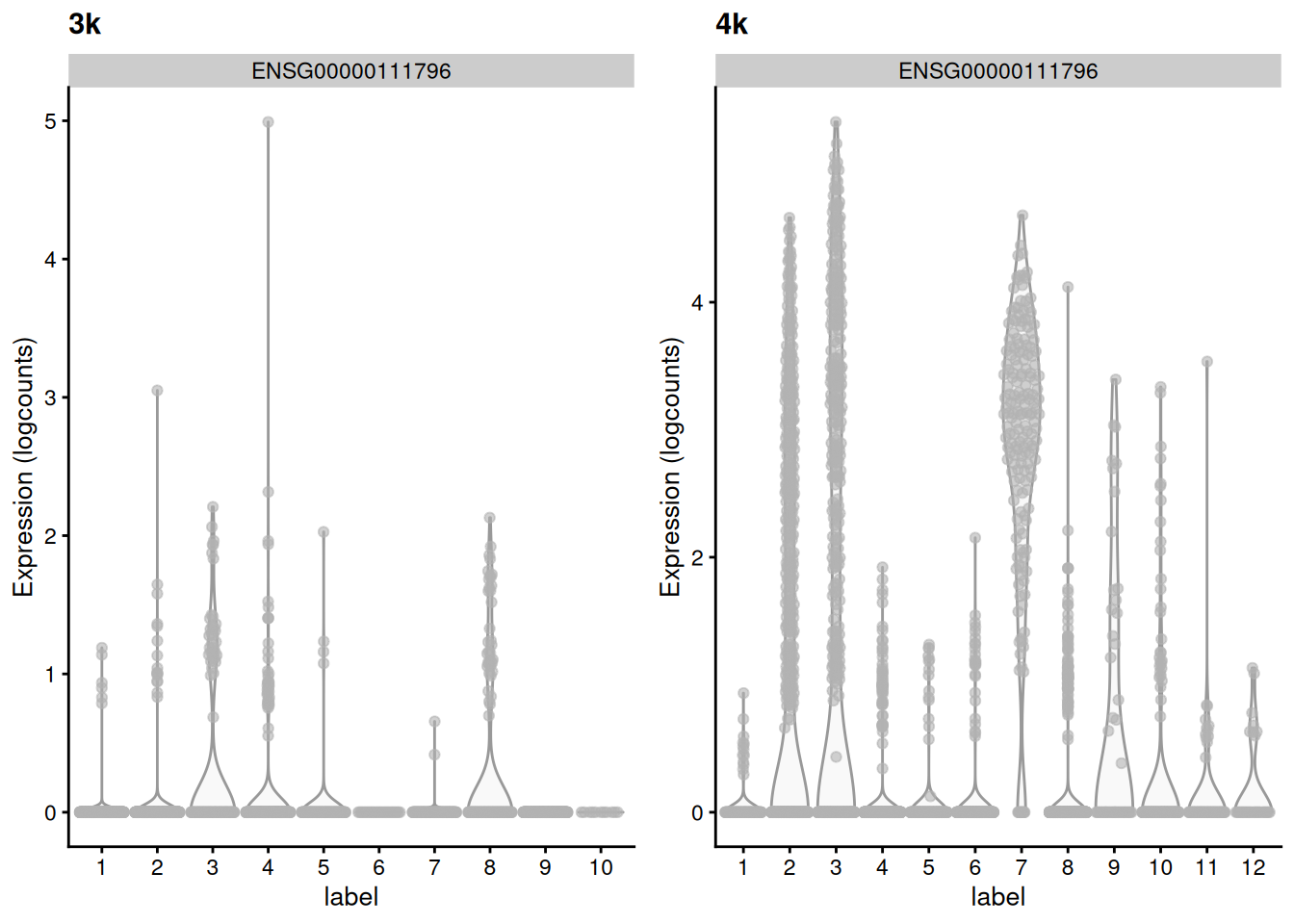
(\#fig:mnn-delta-var-pbmc)Distribution of the expression of the gene with the largest variance of MNN pair differences in each batch of the the PBMC dataset.
```
R Under development (unstable) (2024-10-21 r87258)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.1 LTS
Matrix products: default
BLAS: /home/biocbuild/bbs-3.21-bioc/R/lib/libRblas.so
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.12.0
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_GB LC_COLLATE=C
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
time zone: America/New_York
tzcode source: system (glibc)
attached base packages:
[1] stats4 stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] scater_1.35.0 ggplot2_3.5.1
[3] scuttle_1.17.0 pheatmap_1.0.12
[5] bluster_1.17.0 batchelor_1.23.0
[7] SingleCellExperiment_1.29.1 SummarizedExperiment_1.37.0
[9] Biobase_2.67.0 GenomicRanges_1.59.1
[11] GenomeInfoDb_1.43.2 IRanges_2.41.2
[13] S4Vectors_0.45.2 BiocGenerics_0.53.3
[15] generics_0.1.3 MatrixGenerics_1.19.1
[17] matrixStats_1.5.0 BiocStyle_2.35.0
[19] rebook_1.17.0
loaded via a namespace (and not attached):
[1] gridExtra_2.3 CodeDepends_0.6.6
[3] rlang_1.1.5 magrittr_2.0.3
[5] compiler_4.5.0 dir.expiry_1.15.0
[7] DelayedMatrixStats_1.29.1 vctrs_0.6.5
[9] pkgconfig_2.0.3 crayon_1.5.3
[11] fastmap_1.2.0 XVector_0.47.2
[13] labeling_0.4.3 rmarkdown_2.29
[15] graph_1.85.1 UCSC.utils_1.3.1
[17] ggbeeswarm_0.7.2 xfun_0.50
[19] cachem_1.1.0 beachmat_2.23.6
[21] jsonlite_1.8.9 rhdf5filters_1.19.0
[23] DelayedArray_0.33.4 Rhdf5lib_1.29.0
[25] BiocParallel_1.41.0 irlba_2.3.5.1
[27] parallel_4.5.0 cluster_2.1.8
[29] R6_2.5.1 bslib_0.8.0
[31] RColorBrewer_1.1-3 limma_3.63.3
[33] jquerylib_0.1.4 Rcpp_1.0.14
[35] bookdown_0.42 knitr_1.49
[37] Matrix_1.7-1 igraph_2.1.3
[39] tidyselect_1.2.1 abind_1.4-8
[41] yaml_2.3.10 viridis_0.6.5
[43] codetools_0.2-20 lattice_0.22-6
[45] tibble_3.2.1 withr_3.0.2
[47] evaluate_1.0.3 pillar_1.10.1
[49] BiocManager_1.30.25 filelock_1.0.3
[51] sparseMatrixStats_1.19.0 munsell_0.5.1
[53] scales_1.3.0 glue_1.8.0
[55] metapod_1.15.0 tools_4.5.0
[57] BiocNeighbors_2.1.2 ScaledMatrix_1.15.0
[59] locfit_1.5-9.10 scran_1.35.0
[61] XML_3.99-0.18 cowplot_1.1.3
[63] rhdf5_2.51.2 grid_4.5.0
[65] edgeR_4.5.1 colorspace_2.1-1
[67] GenomeInfoDbData_1.2.13 beeswarm_0.4.0
[69] BiocSingular_1.23.0 HDF5Array_1.35.7
[71] vipor_0.4.7 cli_3.6.3
[73] rsvd_1.0.5 S4Arrays_1.7.1
[75] viridisLite_0.4.2 dplyr_1.1.4
[77] ResidualMatrix_1.17.0 gtable_0.3.6
[79] sass_0.4.9 digest_0.6.37
[81] ggrepel_0.9.6 SparseArray_1.7.4
[83] dqrng_0.4.1 farver_2.1.2
[85] htmltools_0.5.8.1 lifecycle_1.0.4
[87] httr_1.4.7 statmod_1.5.0
```