Chapter 4 DE analyses between conditions
4.1 Motivation
A powerful use of scRNA-seq technology lies in the design of replicated multi-condition experiments to detect population-specific changes in expression between conditions. For example, a researcher could use this strategy to detect gene expression changes for each cell type after drug treatment (Richard et al. 2018) or genetic modifications (Scialdone et al. 2016). This provides more biological insight than conventional scRNA-seq experiments involving only one biological condition, especially if we can relate population changes to specific experimental perturbations. Here, we will focus on differential expression analyses of replicated multi-condition scRNA-seq experiments. Our aim is to find significant changes in expression between conditions for cells of the same type that are present in both conditions.
4.2 Setting up the data
Our demonstration scRNA-seq dataset was generated from chimeric mouse embryos at the E8.5 developmental stage (Pijuan-Sala et al. 2019). Each chimeric embryo was generated by injecting td-Tomato-positive embryonic stem cells (ESCs) into a wild-type (WT) blastocyst. Unlike in previous experiments (Scialdone et al. 2016), there is no genetic difference between the injected and background cells other than the expression of td-Tomato in the former. Instead, the aim of this “wild-type chimera” study is to determine whether the injection procedure itself introduces differences in lineage commitment compared to the background cells.
The experiment used a paired design with three replicate batches of two samples each. Specifically, each batch contains one sample consisting of td-Tomato positive cells and another consisting of negative cells, obtained by fluorescence-activated cell sorting from a single pool of dissociated cells from 6-7 chimeric embryos. For each sample, scRNA-seq data was generated using the 10X Genomics protocol (Zheng et al. 2017) to obtain 2000-7000 cells.
#--- loading ---#
library(MouseGastrulationData)
sce.chimera <- WTChimeraData(samples=5:10)
sce.chimera
#--- feature-annotation ---#
library(scater)
rownames(sce.chimera) <- uniquifyFeatureNames(
rowData(sce.chimera)$ENSEMBL, rowData(sce.chimera)$SYMBOL)
#--- quality-control ---#
drop <- sce.chimera$celltype.mapped %in% c("stripped", "Doublet")
sce.chimera <- sce.chimera[,!drop]
#--- normalization ---#
sce.chimera <- logNormCounts(sce.chimera)
#--- variance-modelling ---#
library(scran)
dec.chimera <- modelGeneVar(sce.chimera, block=sce.chimera$sample)
chosen.hvgs <- dec.chimera$bio > 0
#--- merging ---#
library(batchelor)
set.seed(01001001)
merged <- correctExperiments(sce.chimera,
batch=sce.chimera$sample,
subset.row=chosen.hvgs,
PARAM=FastMnnParam(
merge.order=list(
list(1,3,5), # WT (3 replicates)
list(2,4,6) # td-Tomato (3 replicates)
)
)
)
#--- clustering ---#
g <- buildSNNGraph(merged, use.dimred="corrected")
clusters <- igraph::cluster_louvain(g)
colLabels(merged) <- factor(clusters$membership)
#--- dimensionality-reduction ---#
merged <- runTSNE(merged, dimred="corrected", external_neighbors=TRUE)
merged <- runUMAP(merged, dimred="corrected", external_neighbors=TRUE)## class: SingleCellExperiment
## dim: 14700 19426
## metadata(2): merge.info pca.info
## assays(3): reconstructed counts logcounts
## rownames(14700): Xkr4 Rp1 ... Vmn2r122 CAAA01147332.1
## rowData names(3): rotation ENSEMBL SYMBOL
## colnames(19426): cell_9769 cell_9770 ... cell_30701 cell_30702
## colData names(13): batch cell ... sizeFactor label## reducedDimNames(5): corrected pca.corrected.E7.5 pca.corrected.E8.5
## TSNE UMAP
## mainExpName: NULL
## altExpNames(0):The differential analyses in this chapter will be predicated on many of the pre-processing steps covered previously. For brevity, we will not explicitly repeat them here, only noting that we have already merged cells from all samples into the same coordinate system (Chapter 1) and clustered the merged dataset to obtain a common partitioning across all samples (Basic Chapter 5). A brief inspection of the results indicates that clusters contain similar contributions from all batches with only modest differences associated with td-Tomato expression (Figure 4.1).
##
## FALSE TRUE
## 1 146 300
## 2 362 509
## 3 412 622
## 4 987 674
## 5 598 532
## 6 906 1107
## 7 545 405
## 8 471 399
## 9 256 322
## 10 72 183
## 11 235 196
## 12 254 247
## 13 565 412
## 14 420 310
## 15 1144 549
## 16 469 208
## 17 613 617
## 18 602 571
## 19 247 242
## 20 217 219
## 21 155 1
## 22 61 50
## 23 266 201
## 24 47 57
## 25 82 78
## 26 141 84
## 27 58 0##
## 3 4 5
## 1 107 115 224
## 2 183 242 446
## 3 112 286 636
## 4 224 618 819
## 5 144 646 340
## 6 259 552 1202
## 7 226 175 549
## 8 227 173 470
## 9 102 108 368
## 10 116 54 85
## 11 157 81 193
## 12 186 113 202
## 13 225 227 525
## 14 179 169 382
## 15 153 603 937
## 16 76 161 440
## 17 227 407 596
## 18 112 285 776
## 19 77 156 256
## 20 80 99 257
## 21 6 84 66
## 22 24 30 57
## 23 74 139 254
## 24 16 31 57
## 25 27 29 104
## 26 3 10 212
## 27 2 51 5gridExtra::grid.arrange(
plotTSNE(merged, colour_by="tomato", text_by="label"),
plotTSNE(merged, colour_by=data.frame(pool=factor(merged$pool))),
ncol=2
)
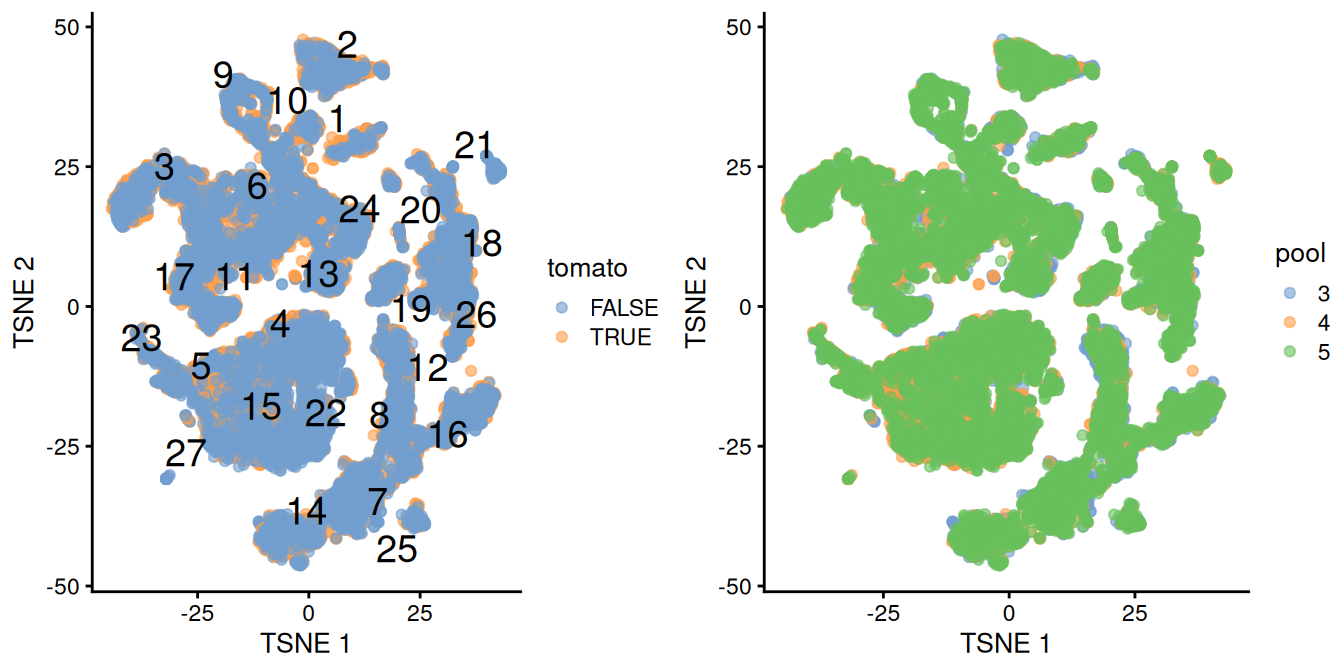
Figure 4.1: \(t\)-SNE plot of the WT chimeric dataset, where each point represents a cell and is colored according to td-Tomato expression (left) or batch of origin (right). Cluster numbers are superimposed based on the median coordinate of cells assigned to that cluster.
Ordinarily, we would be obliged to perform marker detection to assign biological meaning to these clusters. For simplicity, we will skip this step by directly using the existing cell type labels provided by Pijuan-Sala et al. (2019). These were obtained by mapping the cells in this dataset to a larger, pre-annotated “atlas” of mouse early embryonic development. While there are obvious similarities, we see that many of our clusters map to multiple labels and vice versa (Figure 4.2), which reflects the difficulties in unambiguously resolving cell types undergoing differentiation.
## [1] 0.5848by.label <- table(colLabels(merged), merged$celltype.mapped)
pheatmap::pheatmap(log2(by.label+1), color=viridis::viridis(101))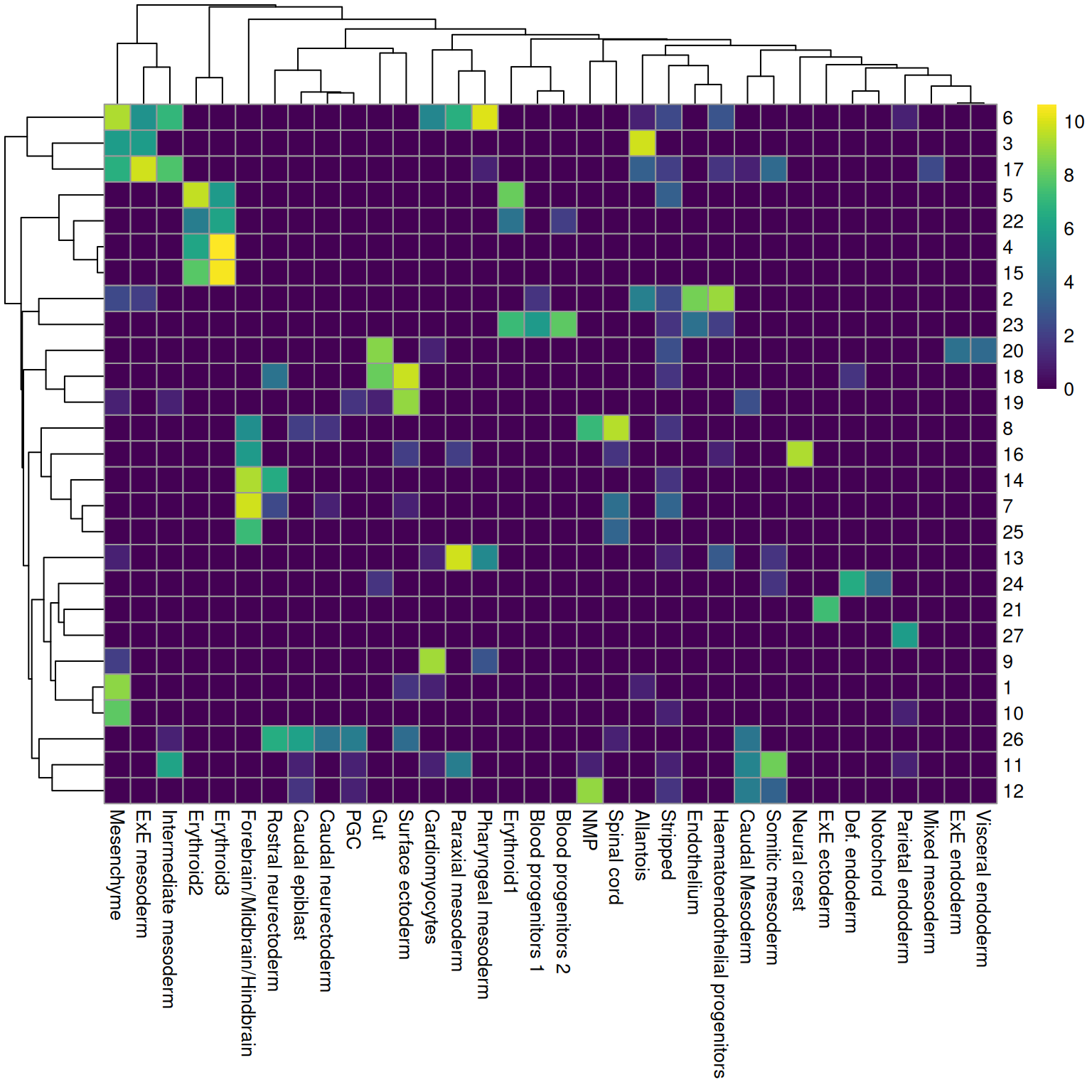
Figure 4.2: Heatmap showing the abundance of cells with each combination of cluster (row) and cell type label (column). The color scale represents the log2-count for each combination.
4.3 Creating pseudo-bulk samples
The most obvious differential analysis is to look for changes in expression between conditions. We perform the DE analysis separately for each label to identify cell type-specific transcriptional effects of injection. The actual DE testing is performed on “pseudo-bulk” expression profiles (Tung et al. 2017), generated by summing counts together for all cells with the same combination of label and sample. This leverages the resolution offered by single-cell technologies to define the labels, and combines it with the statistical rigor of existing methods for DE analyses involving a small number of samples.
# Using 'label' and 'sample' as our two factors; each column of the output
# corresponds to one unique combination of these two factors.
summed <- aggregateAcrossCells(merged,
id=colData(merged)[,c("celltype.mapped", "sample")])
summed## class: SingleCellExperiment
## dim: 14700 186
## metadata(2): merge.info pca.info
## assays(1): counts
## rownames(14700): Xkr4 Rp1 ... Vmn2r122 CAAA01147332.1
## rowData names(3): rotation ENSEMBL SYMBOL
## colnames: NULL
## colData names(16): batch cell ... sample ncells
## reducedDimNames(5): corrected pca.corrected.E7.5 pca.corrected.E8.5
## TSNE UMAP
## mainExpName: NULL
## altExpNames(0):At this point, it is worth reflecting on the motivations behind the use of pseudo-bulking:
- Larger counts are more amenable to standard DE analysis pipelines designed for bulk RNA-seq data. Normalization is more straightforward and certain statistical approximations are more accurate e.g., the saddlepoint approximation for quasi-likelihood methods or normality for linear models.
- Collapsing cells into samples reflects the fact that our biological replication occurs at the sample level (A. T. L. Lun and Marioni 2017). Each sample is represented no more than once for each condition, avoiding problems from unmodelled correlations between samples. Supplying the per-cell counts directly to a DE analysis pipeline would imply that each cell is an independent biological replicate, which is not true from an experimental perspective. (A mixed effects model can handle this variance structure but involves extra statistical and computational complexity for little benefit, see Crowell et al. (2019).)
- Variance between cells within each sample is masked, provided it does not affect variance across (replicate) samples. This avoids penalizing DEGs that are not uniformly up- or down-regulated for all cells in all samples of one condition. Masking is generally desirable as DEGs - unlike marker genes - do not need to have low within-sample variance to be interesting, e.g., if the treatment effect is consistent across replicate populations but heterogeneous on a per-cell basis. Of course, high per-cell variability will still result in weaker DE if it affects the variability across populations, while homogeneous per-cell responses will result in stronger DE due to a larger population-level log-fold change. These effects are also largely desirable.
4.4 Performing the DE analysis
Our DE analysis will be performed using quasi-likelihood (QL) methods from the edgeR package (Robinson, McCarthy, and Smyth 2010; Chen, Lun, and Smyth 2016). This uses a negative binomial generalized linear model (NB GLM) to handle overdispersed count data in experiments with limited replication. In our case, we have biological variation with three paired replicates per condition, so edgeR or its contemporaries is a natural choice for the analysis.
We do not use all labels for GLM fitting as the strong DE between labels makes it difficult to compute a sensible average abundance to model the mean-dispersion trend. Moreover, label-specific batch effects would not be easily handled with a single additive term in the design matrix for the batch. Instead, we arbitrarily pick one of the labels to use for this demonstration.
label <- "Mesenchyme"
current <- summed[,label==summed$celltype.mapped]
# Creating up a DGEList object for use in edgeR:
library(edgeR)
y <- DGEList(counts(current), samples=colData(current))
y## An object of class "DGEList"
## $counts
## Sample1 Sample2 Sample3 Sample4 Sample5 Sample6
## Xkr4 2 0 0 0 3 0
## Rp1 0 0 1 0 0 0
## Sox17 7 0 3 0 14 9
## Mrpl15 1420 271 1009 379 1578 749
## Rgs20 3 0 1 1 0 0
## 14695 more rows ...
##
## $samples
## group lib.size norm.factors batch cell barcode sample stage tomato pool
## Sample1 1 4607113 1 5 <NA> <NA> 5 E8.5 TRUE 3
## Sample2 1 1064981 1 6 <NA> <NA> 6 E8.5 FALSE 3
## Sample3 1 2494039 1 7 <NA> <NA> 7 E8.5 TRUE 4
## Sample4 1 1028679 1 8 <NA> <NA> 8 E8.5 FALSE 4
## Sample5 1 4290259 1 9 <NA> <NA> 9 E8.5 TRUE 5
## Sample6 1 1950858 1 10 <NA> <NA> 10 E8.5 FALSE 5
## stage.mapped celltype.mapped closest.cell doub.density sizeFactor label
## Sample1 <NA> Mesenchyme <NA> NA NA <NA>
## Sample2 <NA> Mesenchyme <NA> NA NA <NA>
## Sample3 <NA> Mesenchyme <NA> NA NA <NA>
## Sample4 <NA> Mesenchyme <NA> NA NA <NA>
## Sample5 <NA> Mesenchyme <NA> NA NA <NA>
## Sample6 <NA> Mesenchyme <NA> NA NA <NA>
## celltype.mapped.1 sample.1 ncells
## Sample1 Mesenchyme 5 286
## Sample2 Mesenchyme 6 55
## Sample3 Mesenchyme 7 243
## Sample4 Mesenchyme 8 134
## Sample5 Mesenchyme 9 478
## Sample6 Mesenchyme 10 299A typical step in bulk RNA-seq data analyses is to remove samples with very low library sizes due to failed library preparation or sequencing. The very low counts in these samples can be troublesome in downstream steps such as normalization (Basic Chapter 2) or for some statistical approximations used in the DE analysis. In our situation, this is equivalent to removing label-sample combinations that have very few or lowly-sequenced cells. The exact definition of “very low” will vary, but in this case, we remove combinations containing fewer than 10 cells (Crowell et al. 2019). Alternatively, we could apply the outlier-based strategy described in Basic Chapter 1, but this makes the strong assumption that all label-sample combinations have similar numbers of cells that are sequenced to similar depth. We defer to the usual diagnostics for bulk DE analyses to decide whether a particular pseudo-bulk profile should be removed.
## Mode FALSE
## logical 6Another typical step in bulk RNA-seq analyses is to remove genes that are lowly expressed.
This reduces computational work, improves the accuracy of mean-variance trend modelling and decreases the severity of the multiple testing correction.
Here, we use the filterByExpr() function from edgeR to remove genes that are not expressed above a log-CPM threshold in a minimum number of samples (determined from the size of the smallest treatment group in the experimental design).
## Mode FALSE TRUE
## logical 9011 5689Finally, we correct for composition biases by computing normalization factors with the trimmed mean of M-values method (Robinson and Oshlack 2010). We do not need the bespoke single-cell methods described in Basic Chapter 2, as the counts for our pseudo-bulk samples are large enough to apply bulk normalization methods. (Note that edgeR normalization factors are closely related but not the same as the size factors described elsewhere in this book. Size factors are proportional to the product of the normalization factors and the library sizes.)
## group lib.size norm.factors batch cell barcode sample stage tomato pool
## Sample1 1 4607113 1.0684 5 <NA> <NA> 5 E8.5 TRUE 3
## Sample2 1 1064981 1.0487 6 <NA> <NA> 6 E8.5 FALSE 3
## Sample3 1 2494039 0.9582 7 <NA> <NA> 7 E8.5 TRUE 4
## Sample4 1 1028679 0.9774 8 <NA> <NA> 8 E8.5 FALSE 4
## Sample5 1 4290259 0.9707 9 <NA> <NA> 9 E8.5 TRUE 5
## Sample6 1 1950858 0.9817 10 <NA> <NA> 10 E8.5 FALSE 5
## stage.mapped celltype.mapped closest.cell doub.density sizeFactor label
## Sample1 <NA> Mesenchyme <NA> NA NA <NA>
## Sample2 <NA> Mesenchyme <NA> NA NA <NA>
## Sample3 <NA> Mesenchyme <NA> NA NA <NA>
## Sample4 <NA> Mesenchyme <NA> NA NA <NA>
## Sample5 <NA> Mesenchyme <NA> NA NA <NA>
## Sample6 <NA> Mesenchyme <NA> NA NA <NA>
## celltype.mapped.1 sample.1 ncells
## Sample1 Mesenchyme 5 286
## Sample2 Mesenchyme 6 55
## Sample3 Mesenchyme 7 243
## Sample4 Mesenchyme 8 134
## Sample5 Mesenchyme 9 478
## Sample6 Mesenchyme 10 299As part of the usual diagnostics for a bulk RNA-seq DE analysis, we generate a mean-difference (MD) plot for each normalized pseudo-bulk profile (Figure 4.3). This should exhibit a trumpet shape centered at zero indicating that the normalization successfully removed systematic bias between profiles. Lack of zero-centering or dominant discrete patterns at low abundances may be symptomatic of deeper problems with normalization, possibly due to insufficient cells/reads/UMIs composing a particular pseudo-bulk profile.
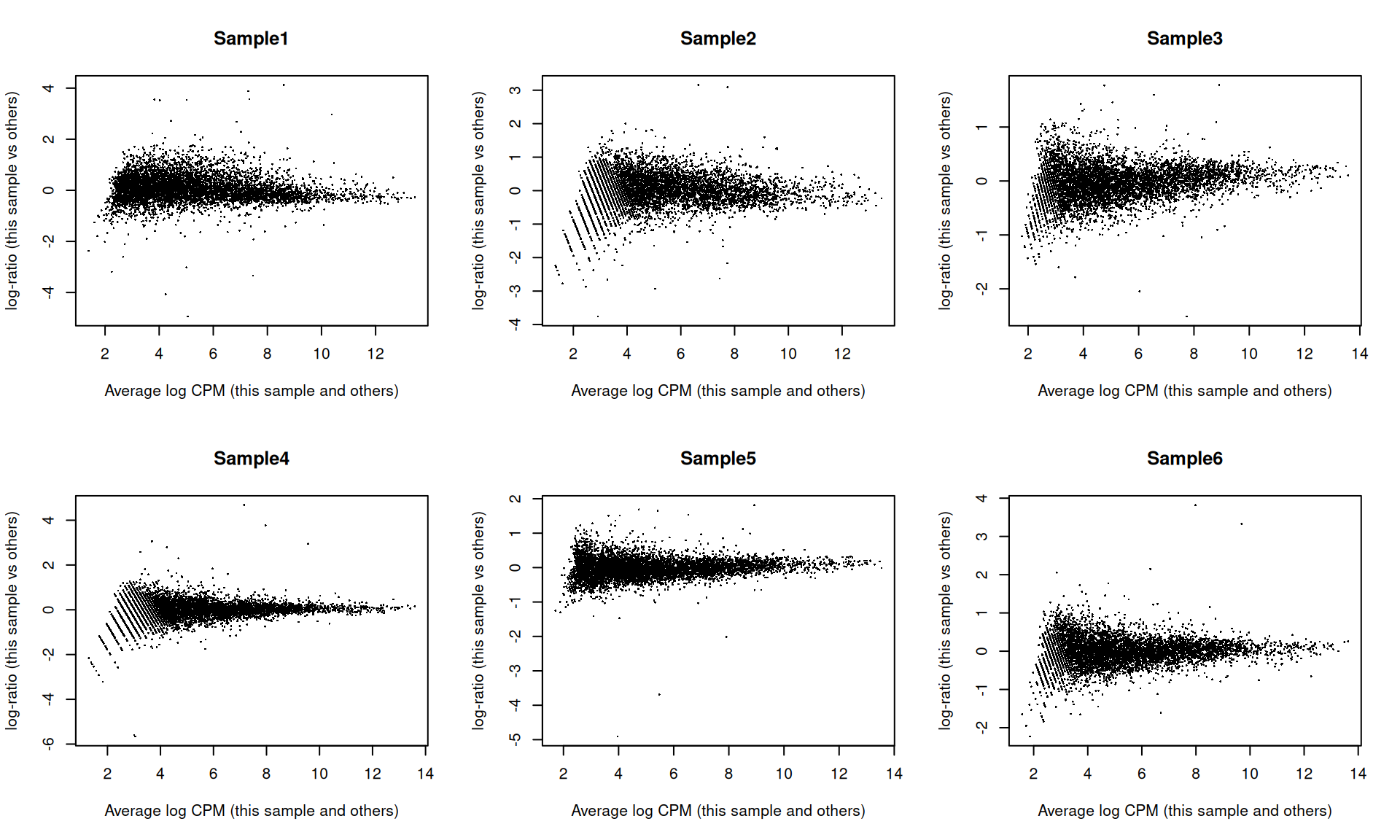
Figure 4.3: Mean-difference plots of the normalized expression values for each pseudo-bulk sample against the average of all other samples.
We also generate a multi-dimensional scaling (MDS) plot for the pseudo-bulk profiles (Figure 4.4). This is closely related to PCA and allows us to visualize the structure of the data in a manner similar to that described in Basic Chapter 4 (though we rarely have enough pseudo-bulk profiles to make use of techniques like \(t\)-SNE). Here, the aim is to check whether samples separate by our known factors of interest - in this case, injection status. Strong separation foreshadows a large number of DEGs in the subsequent analysis.
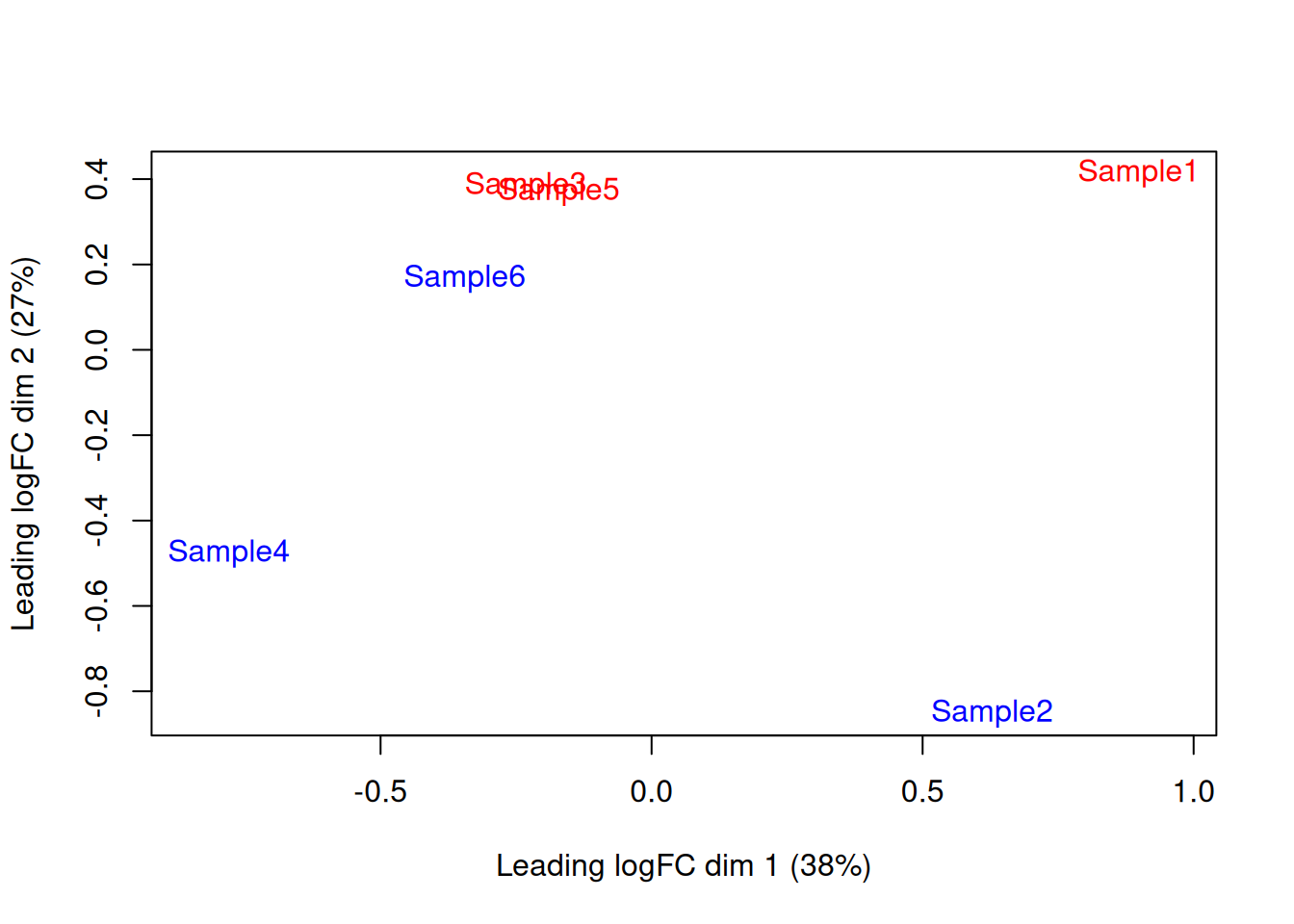
Figure 4.4: MDS plot of the pseudo-bulk log-normalized CPMs, where each point represents a sample and is colored by the tomato status.
We set up the design matrix to block on the batch-to-batch differences across different embryo pools, while retaining an additive term that represents the effect of injection. The latter is represented in our model as the log-fold change in gene expression in td-Tomato-positive cells over their negative counterparts within the same label. Our aim is to test whether this log-fold change is significantly different from zero.
## (Intercept) factor(pool)4 factor(pool)5 factor(tomato)TRUE
## Sample1 1 0 0 1
## Sample2 1 0 0 0
## Sample3 1 1 0 1
## Sample4 1 1 0 0
## Sample5 1 0 1 1
## Sample6 1 0 1 0
## attr(,"assign")
## [1] 0 1 1 2
## attr(,"contrasts")
## attr(,"contrasts")$`factor(pool)`
## [1] "contr.treatment"
##
## attr(,"contrasts")$`factor(tomato)`
## [1] "contr.treatment"We estimate the negative binomial (NB) dispersions with estimateDisp().
The role of the NB dispersion is to model the mean-variance trend (Figure 4.5),
which is not easily accommodated by QL dispersions alone due to the quadratic nature of the NB mean-variance trend.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.0103 0.0167 0.0213 0.0202 0.0234 0.0266
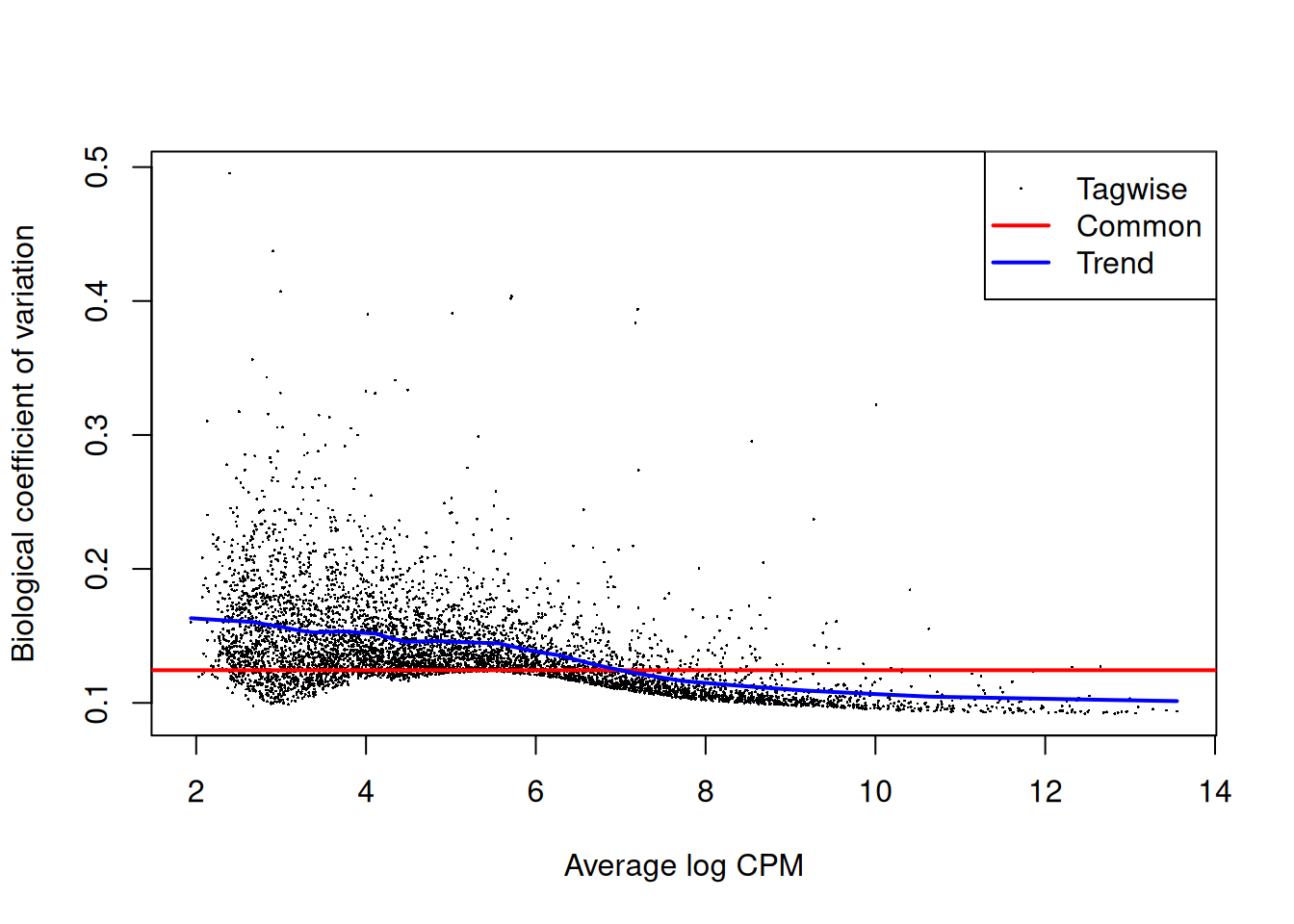
Figure 4.5: Biological coefficient of variation (BCV) for each gene as a function of the average abundance. The BCV is computed as the square root of the NB dispersion after empirical Bayes shrinkage towards the trend. Trended and common BCV estimates are shown in blue and red, respectively.
We also estimate the quasi-likelihood dispersions with glmQLFit() (Chen, Lun, and Smyth 2016).
This fits a GLM to the counts for each gene and estimates the QL dispersion from the GLM deviance.
We set robust=TRUE to avoid distortions from highly variable clusters (Phipson et al. 2016).
The QL dispersion models the uncertainty and variability of the per-gene variance (Figure 4.6) - which is not well handled by the NB dispersions, so the two dispersion types complement each other in the final analysis.
## Length Class Mode
## 0 NULL NULL## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.524 8.076 8.076 8.045 8.076 8.076
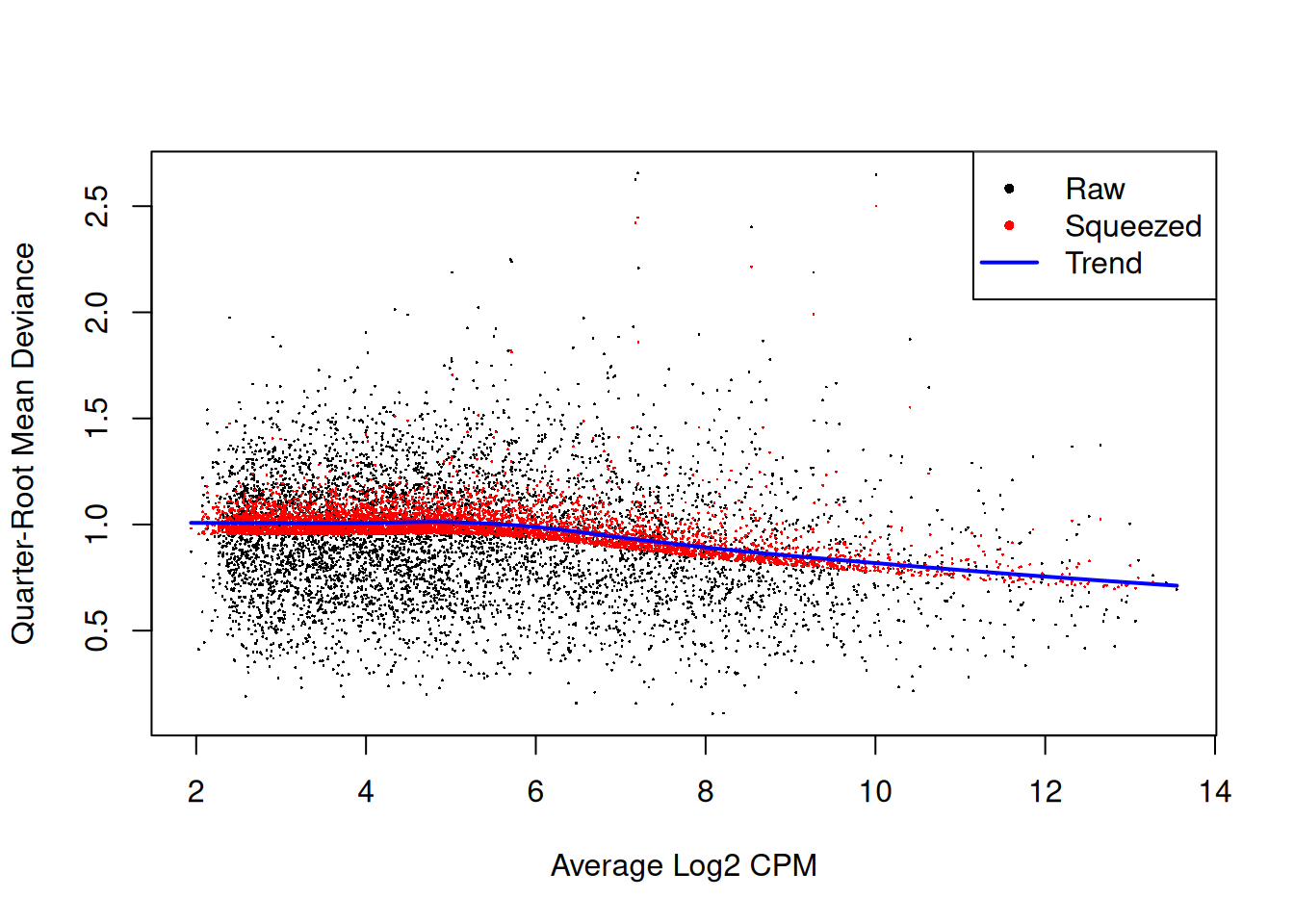
Figure 4.6: QL dispersion estimates for each gene as a function of abundance. Raw estimates (black) are shrunk towards the trend (blue) to yield squeezed estimates (red).
We test for differences in expression due to injection using glmQLFTest().
DEGs are defined as those with non-zero log-fold changes at a false discovery rate of 5%.
Very few genes are significantly DE, indicating that injection has little effect on the transcriptome of mesenchyme cells.
(Note that this logic is somewhat circular,
as a large transcriptional effect may have caused cells of this type to be re-assigned to a different label.
We discuss this in more detail in Section 6.4.1 below.)
## factor(tomato)TRUE
## Down 8
## NotSig 5675
## Up 6## Coefficient: factor(tomato)TRUE
## logFC logCPM F PValue FDR
## Phlda2 -4.3873 9.934 1550.46 2.276e-12 1.295e-08
## Erdr1 2.0685 8.833 345.88 3.937e-09 1.120e-05
## Xist -5.5928 7.522 368.18 2.781e-08 5.273e-05
## Mid1 1.5175 6.931 135.45 3.631e-07 5.165e-04
## Akr1e1 -1.7253 5.128 94.03 1.988e-06 2.262e-03
## H13 -1.0598 7.540 84.78 3.190e-06 2.945e-03
## Kcnq1ot1 1.3798 7.242 80.35 4.069e-06 2.945e-03
## Zdbf2 1.8015 6.797 80.04 4.142e-06 2.945e-03
## Cdkn1c -5.9714 8.678 248.40 5.071e-06 3.205e-03
## Impact 0.8512 7.353 55.90 2.030e-05 1.124e-024.5 Putting it all together
4.5.1 Looping across labels
Now that we have laid out the theory underlying the DE analysis,
we repeat this process for each of the labels to identify injection-induced DE in each cell type.
This is conveniently done using the pseudoBulkDGE() function from scran,
which will loop over all labels and apply the exact analysis described above to each label.
Users can also set method="voom" to perform an equivalent analysis using the voom() pipeline from limma -
see Workflow Section 8.9 for the full set of function calls.
# Removing all pseudo-bulk samples with 'insufficient' cells.
summed.filt <- summed[,summed$ncells >= 10]
library(scran)
de.results <- pseudoBulkDGE(summed.filt,
label=summed.filt$celltype.mapped,
design=~factor(pool) + tomato,
coef="tomatoTRUE",
condition=summed.filt$tomato
)The function returns a list of DataFrames containing the DE results for each label.
Each DataFrame also contains the intermediate edgeR objects used in the DE analyses,
which can be used to generate any of previously described diagnostic plots (Figure 4.7).
It is often wise to generate these plots to ensure that any interesting results are not compromised by technical issues.
## DataFrame with 14700 rows and 5 columns
## logFC logCPM F PValue FDR
## <numeric> <numeric> <numeric> <numeric> <numeric>
## Phlda2 -2.490005 12.58170 1187.603 2.95772e-14 1.42385e-10
## Xist -7.980273 8.00187 1052.935 7.08394e-14 1.70510e-10
## Erdr1 1.945135 9.07313 279.650 3.14612e-10 5.04847e-07
## Slc22a18 -4.339643 4.04375 118.124 5.40064e-08 6.49967e-05
## Slc38a4 0.891213 10.24084 115.478 7.12215e-08 6.85720e-05
## ... ... ... ... ... ...
## Ccl27a_ENSMUSG00000095247 NA NA NA NA NA
## CR974586.5 NA NA NA NA NA
## AC132444.6 NA NA NA NA NA
## Vmn2r122 NA NA NA NA NA
## CAAA01147332.1 NA NA NA NA NA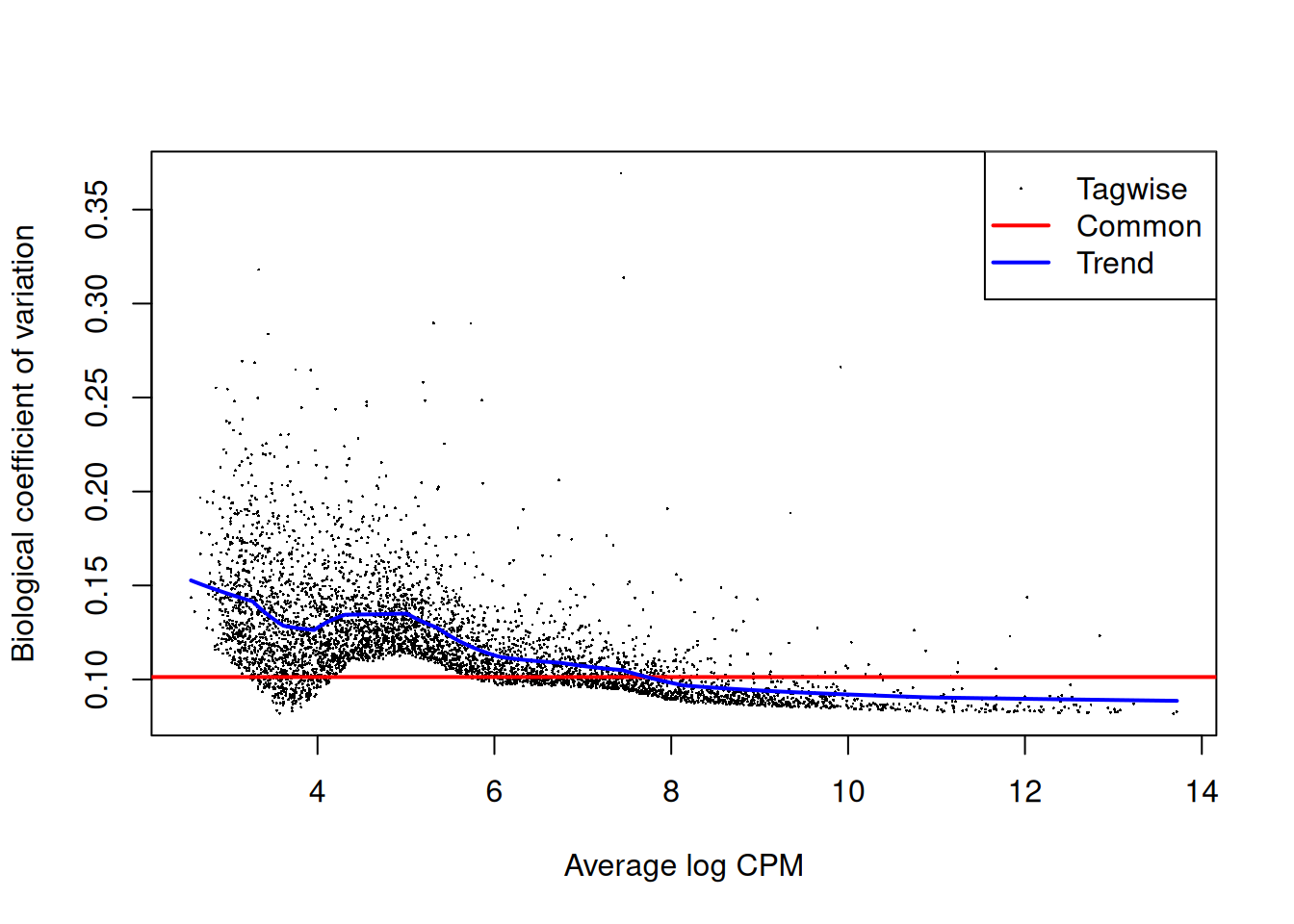
Figure 4.7: Biological coefficient of variation (BCV) for each gene as a function of the average abundance for the allantois pseudo-bulk analysis. Trended and common BCV estimates are shown in blue and red, respectively.
We list the labels that were skipped due to the absence of replicates or contrasts. If it is necessary to extract statistics in the absence of replicates, several strategies can be applied such as reducing the complexity of the model or using a predefined value for the NB dispersion. We refer readers to the edgeR user’s guide for more details.
## [1] "Blood progenitors 1" "Caudal epiblast" "Caudal neurectoderm"
## [4] "ExE ectoderm" "Parietal endoderm" "Stripped"4.5.2 Cross-label meta-analyses
We examine the numbers of DEGs at a FDR of 5% for each label using the decideTestsPerLabel() function.
In general, there seems to be very little differential expression that is introduced by injection.
Note that genes listed as NA were either filtered out as low-abundance genes for a given label’s analysis,
or the comparison of interest was not possible for a particular label,
e.g., due to lack of residual degrees of freedom or an absence of samples from both conditions.
## -1 0 1 NA
## Allantois 20 4778 16 9886
## Blood progenitors 2 8 2463 4 12225
## Cardiomyocytes 4 4364 5 10327
## Caudal Mesoderm 5 1736 3 12956
## Def. endoderm 5 1395 1 13299
## Endothelium 3 3219 9 11469
## Erythroid1 5 2793 6 11896
## Erythroid2 4 3390 9 11297
## Erythroid3 10 5058 10 9622
## ExE mesoderm 2 5098 10 9590
## Forebrain/Midbrain/Hindbrain 8 6227 11 8454
## Gut 5 4483 6 10206
## Haematoendothelial progenitors 5 4102 10 10583
## Intermediate mesoderm 3 3073 4 11620
## Mesenchyme 8 5675 6 9011
## NMP 5 4109 10 10576
## Neural crest 6 3314 5 11375
## Paraxial mesoderm 4 4757 5 9934
## Pharyngeal mesoderm 2 5085 7 9606
## Rostral neurectoderm 4 3336 3 11357
## Somitic mesoderm 4 2959 5 11732
## Spinal cord 5 4595 6 10094
## Surface ectoderm 4 5566 4 9126For each gene, we compute the percentage of cell types in which that gene is upregulated or downregulated upon injection. Here, we consider a gene to be non-DE if it is not retained after filtering. We see that Xist is consistently downregulated in the injected cells; this is consistent with the fact that the injected cells are male while the background cells are derived from pools of male and female embryos, due to experimental difficulties with resolving sex at this stage. The consistent downregulation of Phlda2 and Cdkn1c in the injected cells is also interesting given that both are imprinted genes. However, some of these commonalities may be driven by shared contamination from ambient RNA - we discuss this further in Section 5.
# Upregulated across most cell types.
up.de <- is.de > 0 & !is.na(is.de)
head(sort(rowMeans(up.de), decreasing=TRUE), 10)## Erdr1 Mid1 Kcnq1ot1 Nnat Mcts2 Hopx Slc38a4 Impact
## 1.0000 0.9565 0.7391 0.5217 0.3913 0.3913 0.3913 0.3913
## Zdbf2 Zfp985
## 0.3043 0.1304# Downregulated across cell types.
down.de <- is.de < 0 & !is.na(is.de)
head(sort(rowMeans(down.de), decreasing=TRUE), 10)## Cdkn1c Xist Phlda2 Akr1e1 H13 Wfdc2 Mfap2 Asb4 Dqx1 Gm15915
## 0.86957 0.82609 0.78261 0.69565 0.43478 0.17391 0.08696 0.08696 0.08696 0.08696To identify label-specific DE, we use the pseudoBulkSpecific() function to test for significant differences from the average log-fold change over all other labels.
More specifically, the null hypothesis for each label and gene is that the log-fold change lies between zero and the average log-fold change of the other labels.
If a gene rejects this null for our label of interest, we can conclude that it exhibits DE that is more extreme or of the opposite sign compared to that in the majority of other labels (Figure 4.8).
This approach is effectively a poor man’s interaction model that sacrifices the uncertainty of the average for an easier compute.
We note that, while the difference from the average is a good heuristic, there is no guarantee that the top genes are truly label-specific; comparable DE in a subset of the other labels may be offset by weaker effects when computing the average.
de.specific <- pseudoBulkSpecific(summed.filt,
label=summed.filt$celltype.mapped,
design=~factor(pool) + tomato,
coef="tomatoTRUE",
condition=summed.filt$tomato
)
cur.specific <- de.specific[["Allantois"]]
cur.specific <- cur.specific[order(cur.specific$PValue),]
cur.specific## DataFrame with 14700 rows and 6 columns
## logFC logCPM F PValue FDR
## <numeric> <numeric> <numeric> <numeric> <numeric>
## Slc22a18 -4.339643 4.04375 118.1237 5.40064e-08 0.000259987
## Acta2 -0.830956 9.12478 49.4532 1.13714e-05 0.022307775
## Mxd4 -1.421817 5.64602 56.4106 1.39018e-05 0.022307775
## Rbp4 1.888963 4.35443 33.8495 5.55534e-05 0.066858484
## Myl9 -0.987609 6.24832 33.3753 1.55612e-04 0.147458350
## ... ... ... ... ... ...
## Ccl27a_ENSMUSG00000095247 NA NA NA NA NA
## CR974586.5 NA NA NA NA NA
## AC132444.6 NA NA NA NA NA
## Vmn2r122 NA NA NA NA NA
## CAAA01147332.1 NA NA NA NA NA
## OtherAverage
## <numeric>
## Slc22a18 NA
## Acta2 -0.0232029
## Mxd4 -0.1533356
## Rbp4 -0.0881725
## Myl9 -0.0930971
## ... ...
## Ccl27a_ENSMUSG00000095247 NA
## CR974586.5 NA
## AC132444.6 NA
## Vmn2r122 NA
## CAAA01147332.1 NAsizeFactors(summed.filt) <- NULL
plotExpression(logNormCounts(summed.filt),
features="Rbp4",
x="tomato", colour_by="tomato",
other_fields="celltype.mapped") +
facet_wrap(~celltype.mapped)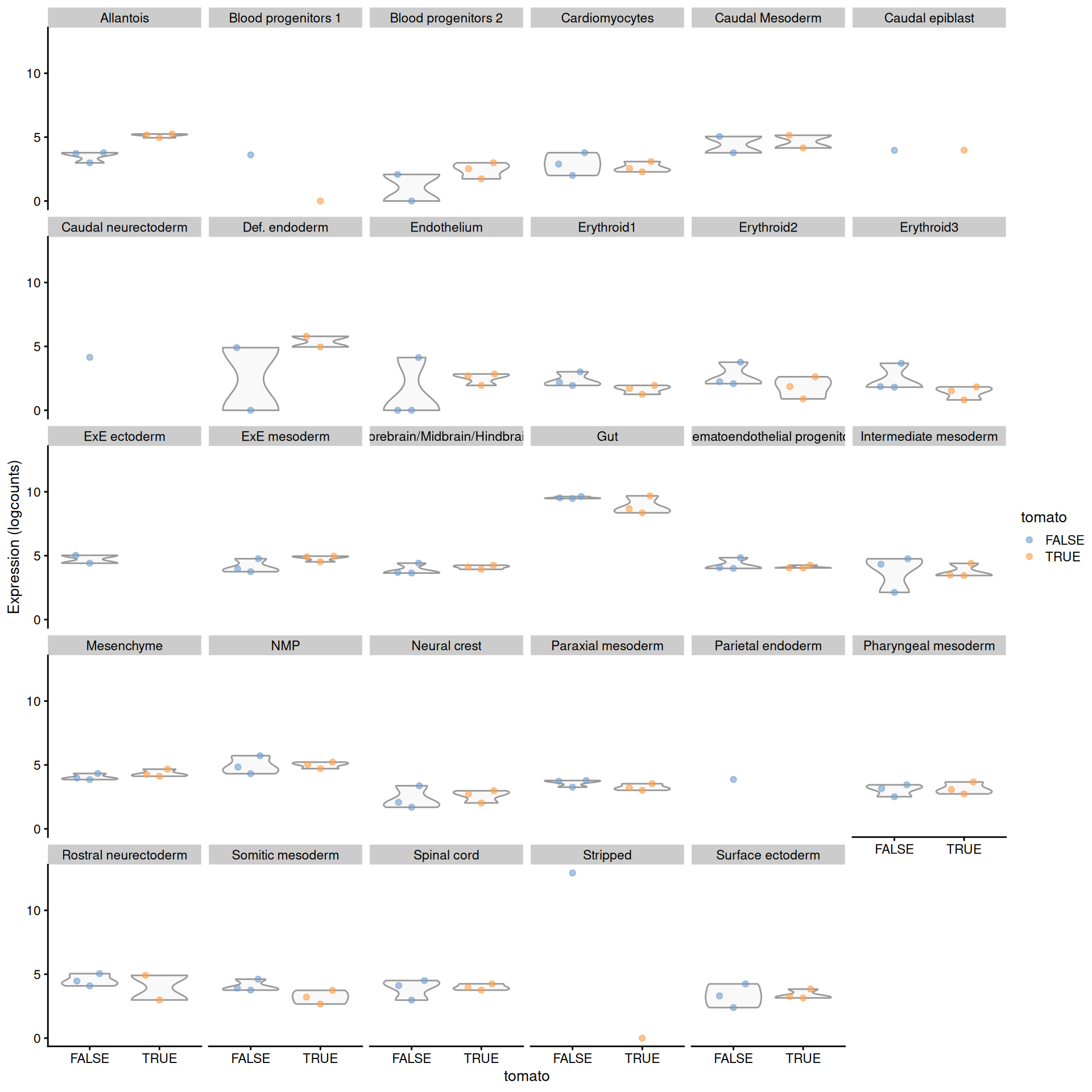
Figure 4.8: Distribution of summed log-expression values for Rbp4 in each label of the chimeric embryo dataset. Each facet represents a label with distributions stratified by injection status.
For greater control over the identification of label-specific DE, we can use the output of decideTestsPerLabel() to identify genes that are significant in our label of interest yet not DE in any other label.
As hypothesis tests are not typically geared towards identifying genes that are not DE, we use an ad hoc approach where we consider a gene to be consistent with the null hypothesis for a label if it fails to be detected at a generous FDR threshold of 50%.
We demonstrate this approach below by identifying injection-induced DE genes that are unique to the allantois.
It is straightforward to tune the selection, e.g., to genes that are DE in no more than 90% of other labels by simply relaxing the threshold used to construct not.de.other, or to genes that are DE across multiple labels of interest but not in the rest, and so on.
# Finding all genes that are not remotely DE in all other labels.
remotely.de <- decideTestsPerLabel(de.results, threshold=0.5)
not.de <- remotely.de==0 | is.na(remotely.de)
not.de.other <- rowMeans(not.de[,colnames(not.de)!="Allantois"])==1
# Intersecting with genes that are DE inthe allantois.
unique.degs <- is.de[,"Allantois"]!=0 & not.de.other
unique.degs <- names(which(unique.degs))
# Inspecting the results.
de.allantois <- de.results$Allantois
de.allantois <- de.allantois[unique.degs,]
de.allantois <- de.allantois[order(de.allantois$PValue),]
de.allantois## DataFrame with 5 rows and 5 columns
## logFC logCPM F PValue FDR
## <numeric> <numeric> <numeric> <numeric> <numeric>
## Slc22a18 -4.339643 4.04375 118.1237 5.40064e-08 6.49967e-05
## Mxd4 -1.421817 5.64602 56.4106 4.19906e-06 2.24603e-03
## Rbp4 1.888963 4.35443 33.8495 5.55534e-05 1.28376e-02
## Cfc1 -0.949597 5.74759 25.1812 2.29009e-04 3.65923e-02
## Cryab -0.985783 5.28419 23.0317 3.38890e-04 4.53171e-02The main caveat is that differences in power between labels require some caution when interpreting label specificity. For example, Figure 4.9 shows that the top-ranked allantois-specific gene exhibits some evidence of DE in other labels but was not detected for various reasons like low abundance or insufficient replicates. A more correct but complex approach would be to fit a interaction model to the pseudo-bulk profiles for each pair of labels, where the interaction is between the coefficient of interest and the label identity; this is left as an exercise for the reader.
plotExpression(logNormCounts(summed.filt),
features="Slc22a18",
x="tomato", colour_by="tomato",
other_fields="celltype.mapped") +
facet_wrap(~celltype.mapped)
Figure 4.9: Distribution of summed log-expression values for each label in the chimeric embryo dataset. Each facet represents a label with distributions stratified by injection status.
4.6 Testing for between-label differences
The above examples focus on testing for differences in expression between conditions for the same cell type or label.
However, the same methodology can be applied to test for differences between cell types across samples.
This kind of DE analysis overcomes the lack of suitable replication discussed in Advanced Section 6.4.2.
To demonstrate, say we want to test for DEGs between the neural crest and notochord samples.
We subset our summed counts to those two cell types and we run the edgeR workflow via pseudoBulkDGE().
summed.sub <- summed[,summed$celltype.mapped %in% c("Neural crest", "Notochord")]
# Using a dummy value for the label to allow us to include multiple cell types
# in the fitted model; otherwise, each cell type will be processed separately.
between.res <- pseudoBulkDGE(summed.sub,
label=rep("dummy", ncol(summed.sub)),
design=~factor(sample) + celltype.mapped,
coef="celltype.mappedNotochord")[[1]]
table(Sig=between.res$FDR <= 0.05, Sign=sign(between.res$logFC))## Sign
## Sig -1 1
## FALSE 2171 1605
## TRUE 764 237## DataFrame with 14700 rows and 5 columns
## logFC logCPM F PValue
## <numeric> <numeric> <numeric> <numeric>
## T 10.87587 7.07425 547.954 2.47403e-117
## Krt19 8.15955 6.16367 356.152 8.73409e-78
## Krt8 4.39740 8.43123 280.026 7.94616e-62
## Krt18 4.71257 7.65059 267.217 3.98965e-59
## Mest -4.86552 11.98807 243.708 3.71160e-54
## ... ... ... ... ...
## Ccl27a_ENSMUSG00000095247 NA NA NA NA
## CR974586.5 NA NA NA NA
## AC132444.6 NA NA NA NA
## Vmn2r122 NA NA NA NA
## CAAA01147332.1 NA NA NA NA
## FDR
## <numeric>
## T 1.18185e-113
## Krt19 2.08614e-74
## Krt8 1.26529e-58
## Krt18 4.76464e-56
## Mest 3.54607e-51
## ... ...
## Ccl27a_ENSMUSG00000095247 NA
## CR974586.5 NA
## AC132444.6 NA
## Vmn2r122 NA
## CAAA01147332.1 NAWe inspect some of the top hits in more detail (Figure 4.10). As one might expect, these two cell types are quite different.
summed.sub <- logNormCounts(summed.sub, size.factors=NULL)
plotExpression(summed.sub,
features=head(rownames(between.res)[order(between.res$PValue)]),
x="celltype.mapped",
colour_by=I(factor(summed.sub$sample)))
Figure 4.10: Distribution of the log-expression values for the top DEGs between the neural crest and notochord. Each point represents a pseudo-bulk profile and is colored by the sample of origin.
Whether or not this is a scientifically meaningful comparison depends on the nature of the labels. These particular labels were defined by clustering, which means that the presence of DEGs is a foregone conclusion (Advanced Section 6.4). Nonetheless, it may have some utility for applications where the labels are defined using independent information, e.g., from FACS.
The same approach can also be used to test whether the log-fold changes between two labels are significantly different between conditions.
This is equivalent to testing for a significant interaction between each cell’s label and the condition of its sample of origin.
The \(p\)-values are likely to be more sensible here; any artificial differences induced by clustering should cancel out between conditions, leaving behind real (and interesting) differences.
Some extra effort is usually required to obtain a full-rank design matrix -
this is demonstrated below to test for a significant interaction between the notochord/neural crest separation and injection status (tomato).
inter.res <- pseudoBulkDGE(summed.sub,
label=rep("dummy", ncol(summed.sub)),
design=function(df) {
combined <- with(df, paste0(tomato, ".", celltype.mapped))
combined <- make.names(combined)
design <- model.matrix(~0 + factor(sample) + combined, df)
design[,!grepl("Notochord", colnames(design))]
},
coef="combinedTRUE.Neural.crest"
)[[1]]
table(Sig=inter.res$FDR <= 0.05, Sign=sign(inter.res$logFC))## Sign
## Sig -1 0 1
## FALSE 1443 13 3321## DataFrame with 14700 rows and 5 columns
## logFC logCPM F PValue FDR
## <numeric> <numeric> <numeric> <numeric> <numeric>
## Noto -11.28825 7.36866 15.3810 9.55119e-05 0.14941
## Foxj1 -10.98882 6.65952 15.3304 9.80621e-05 0.14941
## Shh -10.74794 5.85831 15.1861 9.81993e-05 0.14941
## Cyb561 -10.45862 5.20446 14.6488 1.30488e-04 0.14941
## Foxa2 -8.48654 6.27993 13.9033 1.93767e-04 0.14941
## ... ... ... ... ... ...
## Ccl27a_ENSMUSG00000095247 NA NA NA NA NA
## CR974586.5 NA NA NA NA NA
## AC132444.6 NA NA NA NA NA
## Vmn2r122 NA NA NA NA NA
## CAAA01147332.1 NA NA NA NA NASession Info
R Under development (unstable) (2024-10-21 r87258)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.1 LTS
Matrix products: default
BLAS: /home/biocbuild/bbs-3.21-bioc/R/lib/libRblas.so
LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.12.0
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_GB LC_COLLATE=C
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=C
[9] LC_ADDRESS=C LC_TELEPHONE=C
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C
time zone: America/New_York
tzcode source: system (glibc)
attached base packages:
[1] stats4 stats graphics grDevices utils datasets methods
[8] base
other attached packages:
[1] scran_1.35.0 edgeR_4.5.1
[3] limma_3.63.3 bluster_1.17.0
[5] scater_1.35.0 ggplot2_3.5.1
[7] scuttle_1.17.0 SingleCellExperiment_1.29.1
[9] SummarizedExperiment_1.37.0 Biobase_2.67.0
[11] GenomicRanges_1.59.1 GenomeInfoDb_1.43.2
[13] IRanges_2.41.2 S4Vectors_0.45.2
[15] BiocGenerics_0.53.3 generics_0.1.3
[17] MatrixGenerics_1.19.1 matrixStats_1.5.0
[19] BiocStyle_2.35.0 rebook_1.17.0
loaded via a namespace (and not attached):
[1] tidyselect_1.2.1 viridisLite_0.4.2 dplyr_1.1.4
[4] vipor_0.4.7 farver_2.1.2 filelock_1.0.3
[7] viridis_0.6.5 fastmap_1.2.0 XML_3.99-0.18
[10] digest_0.6.37 rsvd_1.0.5 lifecycle_1.0.4
[13] cluster_2.1.8 statmod_1.5.0 magrittr_2.0.3
[16] compiler_4.5.0 rlang_1.1.5 sass_0.4.9
[19] tools_4.5.0 igraph_2.1.3 yaml_2.3.10
[22] knitr_1.49 dqrng_0.4.1 S4Arrays_1.7.1
[25] labeling_0.4.3 DelayedArray_0.33.4 RColorBrewer_1.1-3
[28] abind_1.4-8 BiocParallel_1.41.0 withr_3.0.2
[31] CodeDepends_0.6.6 grid_4.5.0 beachmat_2.23.6
[34] colorspace_2.1-1 scales_1.3.0 cli_3.6.3
[37] rmarkdown_2.29 crayon_1.5.3 metapod_1.15.0
[40] httr_1.4.7 ggbeeswarm_0.7.2 cachem_1.1.0
[43] splines_4.5.0 parallel_4.5.0 BiocManager_1.30.25
[46] XVector_0.47.2 vctrs_0.6.5 Matrix_1.7-1
[49] jsonlite_1.8.9 dir.expiry_1.15.0 bookdown_0.42
[52] BiocSingular_1.23.0 BiocNeighbors_2.1.2 ggrepel_0.9.6
[55] irlba_2.3.5.1 beeswarm_0.4.0 locfit_1.5-9.10
[58] jquerylib_0.1.4 glue_1.8.0 codetools_0.2-20
[61] cowplot_1.1.3 gtable_0.3.6 UCSC.utils_1.3.1
[64] ScaledMatrix_1.15.0 munsell_0.5.1 tibble_3.2.1
[67] pillar_1.10.1 htmltools_0.5.8.1 graph_1.85.1
[70] GenomeInfoDbData_1.2.13 R6_2.5.1 evaluate_1.0.3
[73] lattice_0.22-6 pheatmap_1.0.12 bslib_0.8.0
[76] Rcpp_1.0.14 gridExtra_2.3 SparseArray_1.7.4
[79] xfun_0.50 pkgconfig_2.0.3